Kružnica, elipsa, amorfné objekty

Kružnica množina bodov rovnako vzdialených od stredového bodu. Kružnica je najčastejšie definovaná pomocou stredového bodu (x,y) a polomeru r (prípadne bodu, ktorý na nej leží). Rovnicu kružnice môžeme vyjadriť:

1. stredom a polomerom

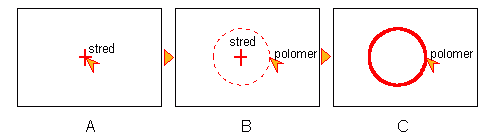
Postup zadávania kružnice stredom a polomerom

2. opísaným štvorcom

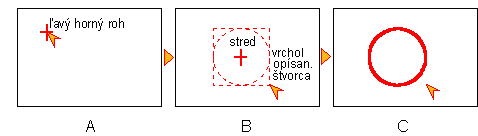
Postup zadávania kružnice opísaným štvorcom

3. Dvomi dotyčnicami reprezentovanými bodmi dotyku a jedným bodom, ktorý určí, do ktorej polroviny sa kružnica vykreslí

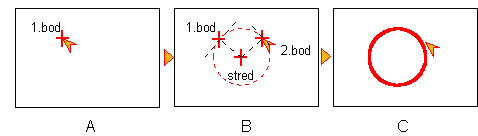
Postup zadávania kružnice dvomi bodmi dotyku

---

Elipsa množina bodov, ktorých súčet vzdialeností od dvoch bodov (ohnísk) je konštantný.
Rovnica elipsy zadanej stredom a polosami rovnobežnými so súradnicovými osami:

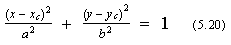
Vykreslenie elipsy sa používa aj na vykreslenie kružnice na zobrazovacie zariadenie, ktoré nemá pomery strán zobrazovacieho priestoru 1:1.

Zadávanie elipsy: je možné elipsu v podstate zadať len opísaným obdĺžnikom a to s buď priebežne kreslenou elipsou alebo príslušným obdĺžnikom.

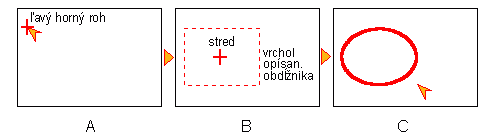
Postup zadávania elipsy opísaným obdĺžnikom

Amorfné objekty – beziérové krivky sú jednoznačne určené smernicami dotyčníc v koncových bodoch priamky

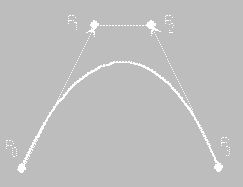
Beziérová krivka

Amorfné objekty – spline krivky predstavujú priebeh funkcie ktorá je v svojich diskrétnych častiach definovaná rôznymi polynómami. Ako bolo povedané je spline vlastne zložená z polynómov. Z bodov, cez ktoré má daná spline funkcia prechádzať a z podmienok spojitosti prvej a druhej derivácie dostaneme rovnice, z ktorých vieme vypočítať neznáme koeficienty výsledného polynómu.

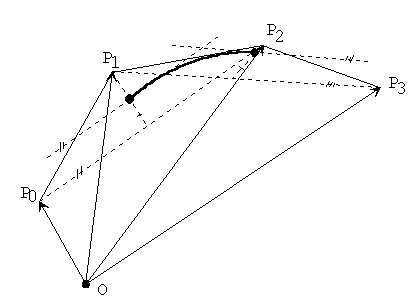
B-spline krivka

Zadavanie spline kriviek:

1. koncovými bodmi, editor určuje zaoblenie a následne sa interaktívne uchopia riadiace body a manuálne sa mení zaoblenie alebo

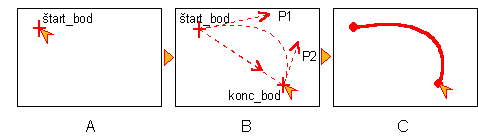
Postup zadávania Beziérovej krivky koncovými bodmi

2. množinou bodov od štartovacieho cez P1 a P2 po koncový bod a následne sa vykreslí krivka. Spravidla sa však používa prvý typ.

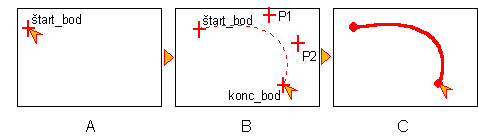
Postup zadávania Beziérovej krivky postupnosťou bodov